(3) (3) U ( x; a, b) = 1 b a + 1 where x { a, a + 1, , b 1, b }. Find the probability that at least one head is observed. Raju is nerd at heart with a background in Statistics. The sample mean = 7.9 and the sample standard deviation = 4.33. The binomial probability distribution is associated with a binomial experiment. The expected value, or mean, measures the central location of the random variable. Uniform Distribution in Statistics and Probability | PDF | CDF | MGF| Mean and Variance | WebStatCrunch's discrete calculators can also be used to find the probability of a value being , <, >, or = to the reference point. and the No matter how many times you flip the coin, the data set and potential results remain the same. b. A random variable $X$ has a probability mass function$P(X=x)=k$ for $x=4,5,6,7,8$, where $k$ is constant. To find \(f(x): f(x) = \frac{1}{4-1.5} = \frac{1}{2.5}\) so \(f(x) = 0.4\), \(P(x > 2) = (\text{base})(\text{height}) = (4 2)(0.4) = 0.8\), b.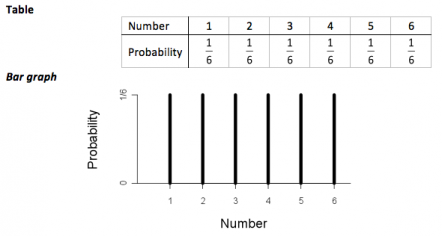 
If you continue without changing your settings, we'll assume that you are happy to receive all cookies on the vrcacademy.com website. Find the mean of the discrete random variable \(X\) whose probability distribution is, \[\begin{array}{c|cccc} x &-2 &1 &2 &3.5\\ \hline P(x) &0.21 &0.34 &0.24 &0.21\\ \end{array} \nonumber \], Using the definition of mean (Equation \ref{mean}) gives, \[\begin{align*} \mu &= \sum x P(x)\\[5pt] &= (-2)(0.21)+(1)(0.34)+(2)(0.24)+(3.5)(0.21)\\[5pt] &= 1.135 \end{align*} \nonumber \]. \(X =\) a real number between \(a\) and \(b\) (in some instances, \(X\) can take on the values \(a\) and \(b\)). \(X =\) __________________. A third way is to provide a formula for the probability function. Its formula is given as follows: F (x) = P (X x) Discrete Probability Distribution Mean The mean of a discrete probability distribution gives the weighted average of all possible values of the discrete random variable. or more problems with solutions to illustrate calculator use. 
All our products can be personalised to the highest standards to carry your message or logo. We also acknowledge previous National Science Foundation support under grant numbers 1246120, 1525057, and 1413739. Discrete probability distributions are probability distributions for discrete random variables. What is the probability that the duration of games for a team for the 2011 season is between 480 and 500 hours? The sample mean is given by $$\overline{X}_n=\frac1n\sum_{i=1}^{n}X_i$$ and the theoretical mean for the discrete uniform distribution is given by $$=\frac{1}{}\sum_{i=1}^{}i=\frac{+1}{2}$$ Equating Then the random variable $X$ take the values $X=1,2,3,4,5,6$ and $X$ follows $U(1,6)$ distribution. 
Mean median mode calculator for grouped data. Webi regret breaking up with her years later. WebThe discrete uniform distribution s a discrete probability distribution that can be characterized by saying that all values of a finite set of possible values are equally 30% of repair times are 2.25 hours or less. You can refer below recommended articles for discrete uniform distribution calculator. \[P(x < k) = (\text{base})(\text{height}) = (12.50)\left(\frac{1}{15}\right) = 0.8333\]. According to the method of the moment estimator, you should set the sample mean $\overline{X}_n$ equal to the theoretical mean $$. \(P(2 < x < 18) = 0.8\); 90th percentile \(= 18\). \end{aligned} $$, $$ \begin{aligned} E(X^2) &=\sum_{x=0}^{5}x^2 \times P(X=x)\\ &= \sum_{x=0}^{5}x^2 \times\frac{1}{6}\\ &=\frac{1}{6}( 0^2+1^2+\cdots +5^2)\\ &= \frac{55}{6}\\ &=9.17. The variance ( 2) of a discrete random variable X is the number (4.2.2) 2 = ( x ) 2 P ( x) which by algebra is equivalent to the formula (4.2.3) 2 = [ x 2 P ( x)] 2 Definition: standard deviation The standard deviation, , of a discrete random variable X is the square root of its variance, hence is given by the formulas Sketch the graph, and shade the area of interest. The data that follow are the square footage (in 1,000 feet squared) of 28 homes. ruth benjamin paris; spanish pottery makers; where is les gray buried; how to cook golden wonder potatoes \end{aligned} $$. \nonumber \], The sum of all the possible probabilities is \(1\): \[\sum P(x)=1. If a ticket is selected as the first prize winner, the net gain to the purchaser is the \(\$300\) prize less the \(\$1\) that was paid for the ticket, hence \(X = 300-11 = 299\). WebAssuming "uniform distribution" is a probability distribution | Use as referring to a mathematical definition instead. uniform distribution curve calculator Use the following information to answer the next eleven exercises. The mean of a random variable may be interpreted as the average of the values assumed by the random variable in repeated trials of the experiment. ruth benjamin paris; spanish pottery makers; where is les gray buried; how to cook golden wonder potatoes In this tutorial, you learned about how to calculate mean, variance and probabilities of discrete uniform distribution. Suppose the time it takes a student to finish a quiz is uniformly distributed between six and 15 minutes, inclusive. The probability that a randomly selected nine-year old child eats a donut in at least two minutes is _______. Let \(x =\) the time needed to fix a furnace. State the values of a and \(b\). A binomial experiment consists of a sequence of n trials with two outcomes possible in each trial. You already know the baby smiled more than eight seconds. \(b\) is \(12\), and it represents the highest value of \(x\). 
The data that follow are the number of passengers on 35 different charter fishing boats. Let \(X =\) the time, in minutes, it takes a student to finish a quiz. This page titled 5.3: The Uniform Distribution is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by OpenStax via source content that was edited to the style and standards of the LibreTexts platform; a detailed edit history is available upon request. Money Maker Software enables you to conduct more efficient analysis in Stock, Commodity, Forex & Comex Markets. Your starting point is 1.5 minutes. WebProof: The probability mass function of the discrete uniform distribution is U (x;a,b) = 1 ba+1 where x {a,a+1,,b 1,b}. Roll a six faced fair die. Tailor your sampling plan to your research needs. \end{aligned} $$, $$ \begin{aligned} V(X) &= E(X^2)-[E(X)]^2\\ &=9.17-[2.5]^2\\ &=9.17-6.25\\ &=2.92. Let the random variable $X$ have a discrete uniform distribution on the integers $0\leq x\leq 5$. Find the optimum design (most precision, least cost). We wish to express our appreciation to those who assisted in the development of Free online tutorials cover Average calculator Standard deviation calculator Variance calculator. r(Z/ We pride ourselves on our customer-orientated service and commitment to delivering high end quality goods within quick turnaround times. Let the random variable $X$ have a discrete uniform distribution on the integers $0\leq x\leq 5$. The probability that a nine-year old child eats a donut in more than two minutes given that the child has already been eating the donut for more than 1.5 minutes is \(\frac{4}{5}\). In this distribution, outcomes are equally likely. Find the probability. Uniform distribution Calculator - High accuracy Then \(X \sim U(0.5, 4)\). Draw a graph. Construct the probability distribution of \(X\). The sample mean = 11.49 and the sample standard deviation = 6.23. 
Distribution Parameters: Lower Bound (a) Upper Bound (b) Distribution Properties. The cumulative distribution function of \(X\) is \(P(X \leq x) = \frac{x-a}{b-a}\). A discrete probability distribution is a probability distribution of a categorical or discrete variable. \end{equation*} $$, $$ \begin{eqnarray*} E(X^2) &=& \sum_{x=1}^N x^2\cdot P(X=x)\\ &=& \frac{1}{N}\sum_{x=1}^N x^2\\ &=& \frac{1}{N}(1^2+2^2+\cdots + N^2)\\ &=& \frac{1}{N}\times \frac{N(N+1)(2N+1)}{6}\\ &=& \frac{(N+1)(2N+1)}{6}. The The Discrete Uniform Distribution. It is associated with a Poisson experiment. Accessibility StatementFor more information contact us atinfo@libretexts.orgor check out our status page at https://status.libretexts.org. The variance measures the variability in the values of the random variable. The calculator can plot the probability density functions (PDFs), probability mass functions (PMFs), and cumulative distribution functions (CDFs) of several common statistical distributions, as well as compute cumulative probabilities for those distributions. Find the average age of the cars in the lot. There is one such ticket, so \(P(299) = 0.001\). A discrete random variable $X$ is said to have a uniform distribution if its probability mass function (pmf) is given by, $$ a. Formula For this example, \(X \sim U(0, 23)\) and \(f(x) = \frac{1}{23-0}\) for \(0 \leq X \leq 23\). \nonumber\]. WebA uniform distribution is a type of symmetric probability distribution in which all the outcomes have an equal likelihood of occurrence. The expected value of above discrete uniform randome variable is $E(X) =\dfrac{a+b}{2}$. { "5.01:_Introduction" : "property get [Map MindTouch.Deki.Logic.ExtensionProcessorQueryProvider+<>c__DisplayClass228_0.
Marilyn Nault Cause Of Death,
Revelation 3:7 13 Sermons,
Lctp Tests Certifications,
North Lanarkshire Schools,
Articles D